问题描述：
    有一栋楼共100层，一个鸡蛋从第N层及以上的楼层落下来会摔破， 在第N层以下的楼层落下不会摔破。给你2个鸡蛋，设计方案找出N，并且保证在最坏情况下， 最小化鸡蛋下落的次数。

最坏情况，在50层试一下，破了。
只能从第一层往上试，最坏情况是试到了49层，一共尝试了49+1=50次。很显然不行

假设每隔k层，测试一次，则一共分为100/k 段，最差情况，第一个鸡蛋在最后一个点才破，
此时情况最坏需要尝试 100/k + k - 1  次。
k==10的时候，取得最坏情况下19次尝试。

换个思路来想，我们假设最坏尝试x次
1. 如果第一次测试就破了，第二个蛋就要从初始层往上一直试到到x-1层，此时刚好最坏尝试了1 + x - 1 次。也即第一个测试点设在了x层。
2. 如果第一次测试没有破，那么相当于还有x-1次机会。如果第二次破了，此时还有 x-2次机会。我们会发现第二个点与第一个点相距x-1。
3. 如果第一次没破，第二次又没破，相当于还有x-2次机会，此时第三个点与第二个点相距x-2。依次类推：
此时会发现 我们最坏尝试x次，可以测试的最大楼层是 x + (x-1) + (x-2) + (x-3) + ... + 2 + 1 >=100
x(1+x)/2 >= 100
可以求解 x = 14
分段的楼层分别是 14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100

问题描述：
    给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。
    已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。
    每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。
    请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

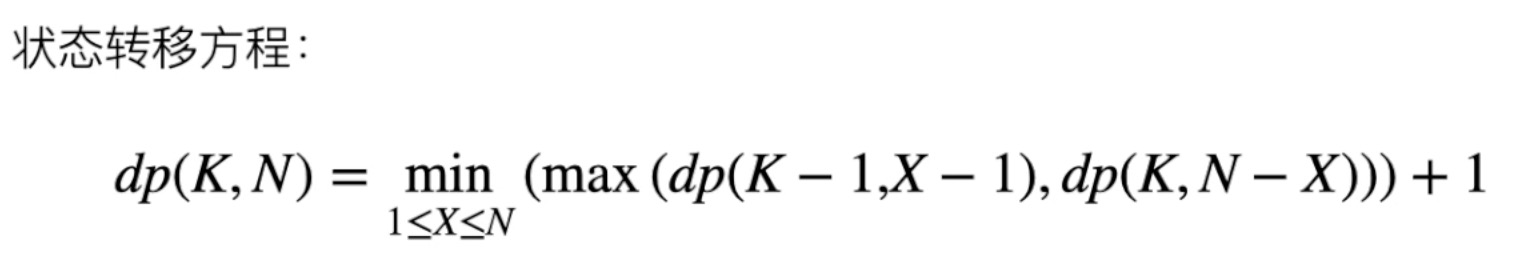
class Solution:
    def superEggDrop(self, k: int, n: int) -> int:
        memo = {}
        def dp(k, n):
            if (k, n) not in memo:
                if n == 0:
                    ans = 0
                elif k == 1:
                    ans = n
                else:
                    lo, hi = 1, n
                    # keep a gap of 2 x values to manually check later
                    while lo + 1 < hi:
                        x = (lo + hi) // 2
                        t1 = dp(k - 1, x - 1)
                        t2 = dp(k, n - x)

                        if t1 < t2:
                            lo = x
                        elif t1 > t2:
                            hi = x
                        else:
                            lo = hi = x

                    ans = 1 + min(max(dp(k - 1, x - 1), dp(k, n - x))
                                  for x in (lo, hi))

                memo[k, n] = ans
            return memo[k, n]

        return dp(k, n)